Passive versus active vibration isolation
Many high resolution measurement systems and experimental setups can be seriously affected by external vibration sources. The dominant source will normally be building vibrations excited by machinery and passing traffic. Acoustic sources can also be troublesome, as can forces introduced directly by the operators hands. With a plethora of solutions available for isolating a system from the environment, how can one decide which is the right solution for a particular application?
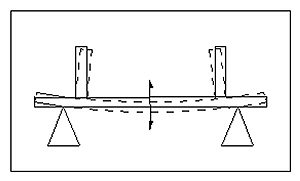
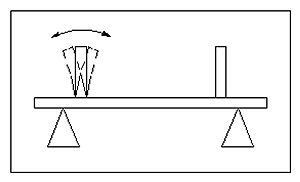
A system can react resonantly and non-resonantly to external vibrations. Consider the case of the interferometer illustrated below.
non-resonant
resonant
A low frequency vertical acceleration of the instrument will cause the structure to distort - the amplitude of this distortion will be proportional to the acceleration and independent of frequency. At higher frequencies structural resonances can be excited. For example a mirror holder can vibrate and thereby modulate the optical path length. In general both effects will be present, but which effect is more important will vary from system to system.
In a system where the structural resonances dominate it will be necessary to isolate against both, building vibrations and acoustic sources. Since these structural resonances come at relatively high frequencies (>50HZ) it is possible to obtain sufficient isolation by mounting the system on rubber inside an acoustic hood. Crude systems using tennis balls or basket balls as isolation elements can be used successfully for such applications - but beware - this is the worst possible 'solution' against low frequency building vibrations.
The vast majority of high resolution measurement instruments react to the distortions introduced by low frequency building vibrations. For isolation against low frequency vibrations the simplest solution is to mount the system on a very soft spring. The transmibility of a slightly damped spring is shown in the curve [A] below.
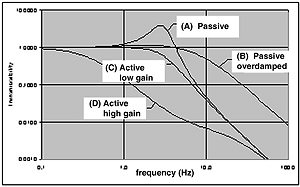
The characteristics of the spring are a transmissibility of unity at the lowest frequency fr. Beyond about 1.4x fr, the spring begins to isolate with the transmission falling off proportional to the square of the frequency. It is important that the frequency fr lies low enough that it is in a region where no significant vibration energy is present. Long elastic cords have been succesfully used, but the system is so resonant and so soft that it takes very long to settle - only students have enough time on their hands! To improve the settling time some damping should be introduced. Air support columns are widely available with optimally damped characteristics. These systems still however have the disadvantage of being very soft and taking several seconds to settle down after a disturbance. Note that is not possible to arbitrarily increase the damping - too much damping as in curve [B] allows the resonance to be removed but the system becomes 'glued' to the floor via the damping medium and can no longer isolate at all!
Active isolation systems offer a solution which combines stiffness with a very short settling time. The most useful active systems employ inertial velocity in a feedback loop. (Inertial velocity can be measured for example by integrating the signal from an accelerometer). A signal proportional to inertial velocity is very similar to a viscous damping force, but with the very important difference that the damping is relative to an inertial plane. So in contrast to the passive system, by increasing the damping as in curve [C] and [D], the system becomes 'glued' to the inerial plane which by definition means the system is isolated from the environment. The more damping the better.
The advantages of active systems over passive ones are many:
- small size
- inherently stiff
- rapid recovery from shock (1-10 ms)
- no air required
- no set-up time
- a performance that is better than that of the best passive systems.
The price is generally modest - and a tiny fraction of the cost of the equipment that will sit on top of the system.
